BFS(Breadth-First Search) : 너비 우선 탐색
- 그래프 완전 탐색
- 시작 노드에서 출발해 시작 노드를 기준으로 가장 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘이다.
- FIFO 탐색 -> Queue 자료구조를 이용한다.
- 목표 노드에 도착하는 경로가 여러개일 때 최단경로를 보장한다.
1. 시간복잡도
인접 리스트
- 노드의 개수가 많고, 간선 수가 적을 때 유리하다.
인접 행렬
- 노드의 개수가 적고, 간선 수가 많을 때 유리하다.
| 인접 리스트 | 인접 행렬 | |
| 특정 간선 검색 | O(degree(N) : 해당 노드의 차수 | O(1) |
| 정점의 차수 계산 | O(degree(N)) | O(N) |
| 전체 노드 탐색 | O(E) | O(N^2) |
| 메모리 | N+E | N^2 |
2. BFS 핵심 이론
1) 방문여부 확인용 배열
- BFS도 DFS와 마찬가지로 한번 방문한 노드를 다시 방문하면 안되므로 노드 방문 여부를 체크할 배열이 필요하다.
- 예를들어 1~6의 노드를 가진 그래프가 있으면,
boolean[] arr = new boolean[7];으로 배열을 만들어 준다.( 0번 인덱스는 사용하지 않는다. ) - 해당 노드를 방문하면 해당 인덱스의 값을 TRUE로 바꿔준다.
2) 원본 그래프 -> 자료구조 초기화(인접리스트)
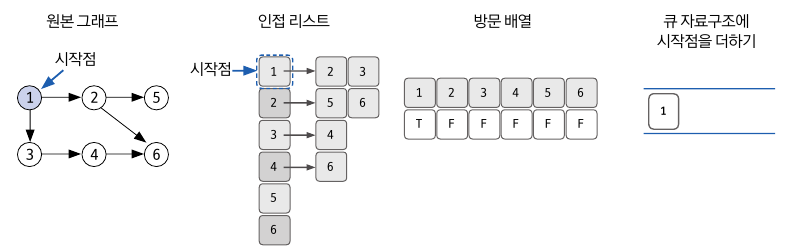
- 시작할 노드를 정한다.
- 각 노드에서 갈수있는 다른 노드를 확인 후 인접리스트로 초기화 한다.
- 시작점을 정했기 때문에 시작점의 방문배열을 T로바꿔주고, Queue에 시작점을 더한다.
3) Queue에서 노드를 꺼낸 노드의 인접노드를 Queue에 삽입
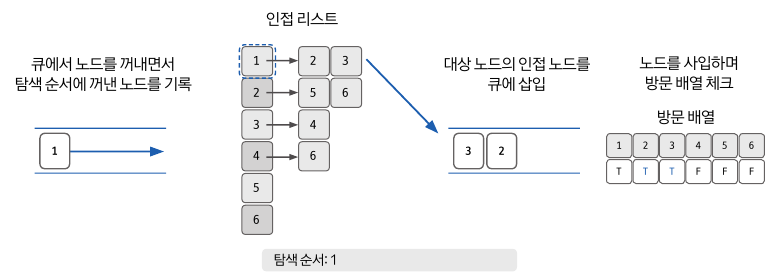
- 맨 처음에 넣었던 노드1을 Queue에서 꺼낸다.
- 꺼낸 노드 1의 인접노드(2,3)을 큐에 삽입한다.
- 이 과정을 Queue가 비워질 때까지 반복한다.
4) 반복
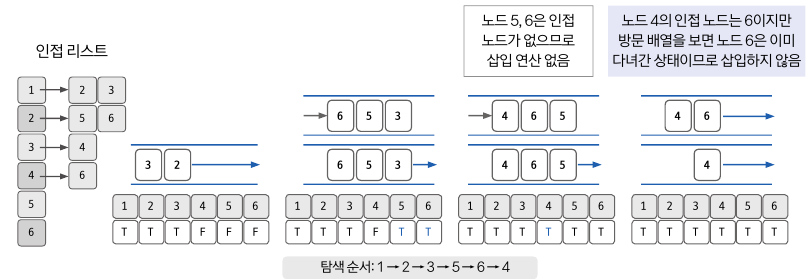
(편의를 위해 poll() 괄호 안에 값을 넣도록 하겠다.)
- 위에서 1을 꺼낸 뒤, 노드2,3을 넣은 상태이다.
poll(2)-> 2의 방문배열 True -> 2의 인접 리스트 5,6을 넣는다.offer(5),offer(6)poll(3)-> 3의 방문배열 True -> 3의 인접 리스트 4를 넣는다.offer(4)poll(5)-> 5의 방문배열 True -> 5의 인접리스트는 없다.poll(6)-> 6의 방문배열 True -> 6의 인접리스트는 없다.poll(4)-> 4의 방문배열 True -> 4의 인접리스트는 없다.queue.isEmpty() == true
3. 구현
static boolean[] visited = new boolean[7]; //방문 배열 초기화
static Queue<Integer> queue = new LinkedList<>();
static ArrayList<Integer>[] A = new ArrayList[7]; //ArrayList 타입 배열 선언
static ArrayList<Integer> procedure = new ArrayList<>(); //탐색 순서 출력을 위한 리스트
public static void main(String[] args){
//ArrayList 형 배열 A 초기화
for(int i=1;i<=6;i++) {
A[i] = new ArrayList<>();//배열의 각 요소마다 ArrayList를 가진다.
}
//위의 예제 인접 리스트 초기화
A[1].add(2);
A[1].add(3);
A[2].add(5);
A[2].add(6);
A[3].add(4);
A[4].add(6);
BFS(1);
System.out.println(procedure.toString()); //[1, 2, 3, 5, 6, 4]
}
private static void BFS(int start){
queue.offer(start);
while(!queue.isEmpty()){
int now = queue.poll();
// poll() 할때, 탐색순서 리스트에 넣어주고,방문배열을 true로 바꿔준다.
procedure.add(now);
visited[now] = true;
// 꺼낸 노드의 인접노드를 전부 확인한다.
for(int i=0;i<A[now].size();i++){
int node = A[now].get(i);
//인접노드가 방문한적 없는 노드면 queue에 넣어준다.
if(!visited[node]){
queue.offer(node);
}
}
}//while문
}//BFS 메소드
}미로찾기
BFS는 위의 예제처럼 그래프를 구성하는 방식도 사용하지만,
지도가 주어지고, 갈수 없는 곳, 갈수 있는곳, 출발위치, 목표위치 등이 주어지는 미로찾기와 같은 형태로도 많이 사용된다.
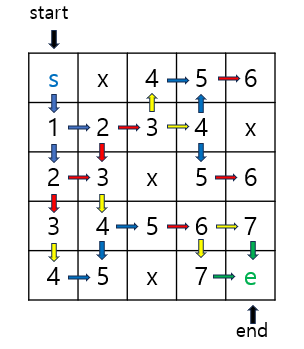
아래와 같이 시작점 s와 목표 지점 e가 주어지고, x는 갈 수 없는 길이라고 생각해보자.
s에서 e까지 가장 빠르게 가는 방법을 알아보자.
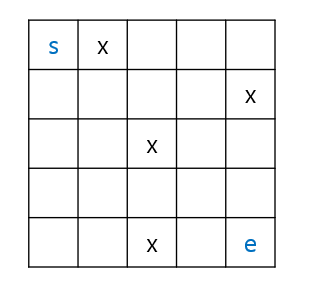
이 문제에서는 4방향으로 이동할 수 있다. 따라서 아래와 같이 갈수 있는 방향을 담은 dirs[][] 배열을 선언해주자.
static int[][] dirs = {{1,0}, {-1,0}, {0,1}, {0,-1}};각 지점에서 4개의 방향을 모두 확인 후, 갈 수 있는 곳인지 아닌지 확인한다.
- 갈 수 있는 곳 : 비어있는 곳
- 갈 수 없는 곳 : x표 되어있는 곳, 인덱스가 0보다 작거나, map.length-1보다 클 때
따라서 아래와 같은 코드로 갈 수 없는 곳을 확인한다. (x표는 -1로 나타냈다.)
//map의 범위를 벗어나는 경우
if(nx < 0 || nx > map.length-1 || ny < 0 || ny > map[0].length-1){
continue;
}
//벽(-1)이거나, 이미 방문한곳( != 0) 일때
if(map[nx][ny] == -1 || map[nx][ny] != 0){
continue;
}모두 하나의 if문에 넣어도 되지만, 이해하기 쉽게 하기 위해 두개의 if문으로 분리했다.
처음에 모두 0(갈수있는 곳)과, -1(갈수 없는 곳, 벽)밖에 없었던 map을 한칸한칸씩 이동할 때마다
이전 값 +1을 하면, 해당 목표위치까지 갈 수 있는 최소 거리가 도출된다.
Code
import java.util.LinkedList;
import java.util.Queue;
public class Main{
static int[][] dirs = {{1,0}, {-1,0}, {0,1}, {0,-1}};
static int bfs(int[][] map, int[] start, int[] end){
Queue<int[]> queue = new LinkedList<>();
queue.offer(start);
while(!queue.isEmpty()){
int[] cur = queue.poll();
int x = cur[0];
int y = cur[1];
for(int[] dir : dirs){
int nx = x + dir[0];
int ny = y + dir[1];
//map의 범위를 벗어나는 경우
if(nx < 0 || nx > map.length-1 || ny < 0 || ny > map[0].length-1){
continue;
}
//벽(-1)이거나, 이미 방문한곳( != 0) 일때
if(map[nx][ny] == -1 || map[nx][ny] != 0){
continue;
}
map[nx][ny] = map[x][y] + 1;
//갈 수 있는 경우, 해당 위치 좌표를 다시 queue에 넣는다.
queue.offer(new int[]{nx, ny});
}
}
return map[end[0]][end[1]];
}
public static void main(String[] args){
int[][] map =
{{0 , -1, 0, 0, 0},
{0, 0, 0, 0, -1},
{0, 0, -1, 0, 0},
{0, 0, 0, 0, 0},
{0, 0, -1, 0, 0}};
int[] start = {0, 0};
int[] end = {4, 4};
int result = bfs(map, start, end);
System.out.println(result); // 8
}
}(이미지 출처) Do it! 알고리즘 코딩 테스트 자바 편 e-book
http://www.yes24.com/Product/Goods/108571508
반응형
'자료구조 & 알고리즘' 카테고리의 다른 글
| [Algorithm/Java] 선택 정렬 (selection sort) (0) | 2023.05.08 |
|---|---|
| [Algorithm/Java] 버블정렬 (bubble sort) (0) | 2023.05.08 |
| [Algorithm/Java] DFS(깊이 우선 탐색) (2) | 2023.05.08 |
| [Java] 배열(Array) (0) | 2023.04.20 |
| [JAVA/자료구조] 컬렉션(Collection) 프레임워크 (0) | 2023.02.07 |
