다익스트라(dijkstra) 알고리즘
다익스트라 알고리즘은 그래프에서 최단거리를 구하는 알고리즘이다.
- 가중치 그래프 상에서 출발노드에서 목표노드까지 이동하는 가장 짧은 경로를 찾는 방법을 찾는다.
- 하나의 출발 노드에서 다른 모든 노드로의 최단 경로를 구할 수 있다.
- 에지(간선)은 모두 양수여야 한다.
- 시간 복잡도 : O(ElogV)
- 그리디와 DP의 특성을 갖고 있다.
다익스트라 알고리즘 동작 원리
1. 인접 리스트로 그래프를 구현한다.
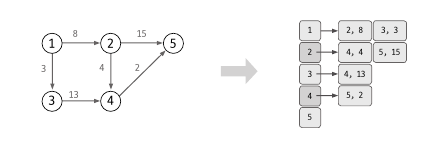
[1] ->[ 2, 8 ] 은 1에서 2로 가는 가중치가 8이라는 뜻이다.
실제로는 아래와 같이 Edge 클래스를 만들어서 Edge 형 ArrayList<>배열을 선언하여 구성하였다.
ArrayList<Edge >[] graph;
class Node{
int to; //가리키는 노드
int weight; //가중치
public Edge (int to, int weight){
this.to = to;
this.weight = weight;
}
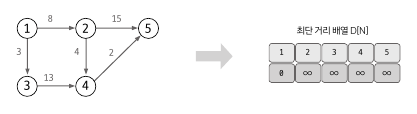
2. 최단거리 배열 초기화 하기
최단거리를 저장할 배열을 만들고, 출발노드는 0, 이외의 노드는 큰 값(Integer.MAX_VALUE)로 초기화 한다.
노드 개수 +1의 배열을 만들어서 0번 인덱스를 사용하지 않는 방법을 이용하면 좋다.
int[] distance = new int[V + 1]; //V : 노드 개수
for(int i = 0; i <= V; i++){
distance[i] = Integer.MAX_VALUE;
}
distance[start] = 0;
3. 현재 값이 가장 작은 노드를 고른다.
최단거리 배열에서 현재 값이 가장 작은 노드를 골라서 업데이트를 시작한다.
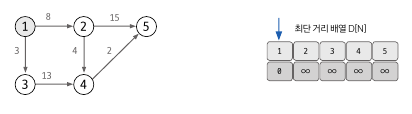
4. 최단거리 배열 업데이트
선택한 노드에 연결 된 에지 값을 바탕으로 다른 노드의 최단거리 배열을 업데이트 한다.
현재 연결된 에지들을 모두 탐색하며 최단거리 배열을 기존 값과 새로운 값중 더 작은 값으로 업데이트 한다.
if(distance[목표 노드] > distance[이전 노드] + 가중치){
distance[목표 노드] = distance[이전 노드] + 가중치;
}5. 과정 3~4를 반복해 최단거리 배열 완성하기
최단거리 배열이 완성될 때 까지 과정 3~4를 반복한다.
아래에서 그 과정을 자세하게 다루겠습니다.

최단거리 배열 완성까지의 과정
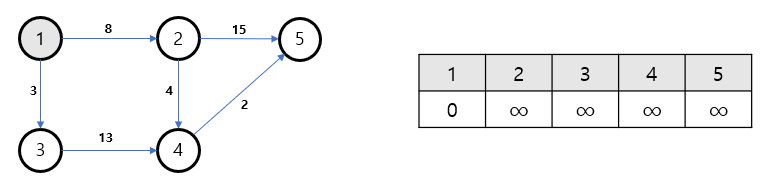
1) 최단거리 배열 초기화 상태
시작점 1에서 출발한다.
1과 인접한 노드 2와 3으로 가는 간선 데이터 [1, 2, 8] , [1, 3, 3]을 확인한다.
2) 2번과 3번노드의 최단거리 배열 업데이트
이전 노드(1번)의 최단거리 배열 값과 현재 간선 데이터의 가중치 값을 더한 값이 현재 간선 목표지점의 최단거리 배열 값보다 작으면 업데이트 해준다.
실제로는 가중치가 작은 값 먼저 나오도록하는 PriorityQueue를 이용해서
(1)->(3) 간선 업데이트 후 (1)->(2) 간선을 업데이트 한다.

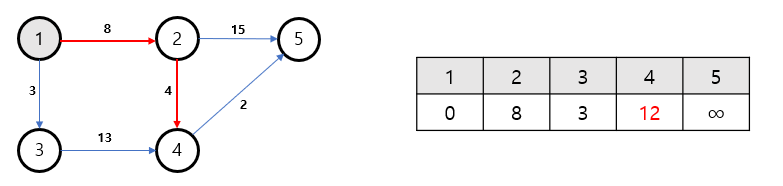
3) (2) -> (4) 최단거리 배열 확인
(2) ->(4) 간선을 확인해보자.
시작점에서 2번노드까지의 거리(8)과 2번 노드에서 4번노드까지의 거리(4)를 더한 값과
4번노드의 최단거리 배열의 값을 비교한다.
- 시작점에서 2번노드까지의 거리(8) + 2번 노드에서 4번노드까지의 거리(4) = 12
- 최단거리 배열의 값 = Infinity
비교 한 결과, 4번 노드의 값을 12로 업데이트 한다.
4) (3) -> (4) 최단거리 배열 확인
(3) ->(4) 간선을 확인해보자.
시작점에서 3번노드까지의 거리(3)과 3번 노드에서 4번노드까지의 거리(13)를 더한 값과
4번노드의 최단거리 배열의 값을 비교한다.
- 시작점에서 3번노드까지의 거리(3) + 3번 노드에서 4번노드까지의 거리(13) = 16
- 최단거리 배열의 값 = 12
비교한 결과, 4번노드의 값은 업데이트 하지 않는다.

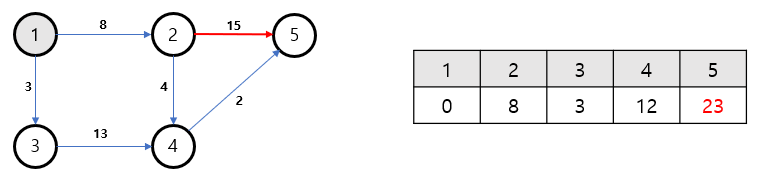
5) (2) -> (5) 최단거리 배열 확인
(2) ->(5) 간선을 확인해보자.
시작점에서 2번노드까지의 거리(8)과 2번 노드에서 5번노드까지의 거리(15)를 더한 값과
5번노드의 최단거리 배열의 값을 비교한다.
- 시작점에서 2번노드까지의 거리(8) + 2번 노드에서 5번노드까지의 거리(15) = 23
- 최단거리 배열의 값 = Infinity
비교한 결과, 5번노드의 값은 23으로 업데이트 한다.
6) (4) -> (5) 최단거리 배열 확인
(4) ->(5) 간선을 확인해보자.
시작점에서 4번노드까지의 거리(12)과 4번 노드에서 5번노드까지의 거리(2)를 더한 값과
5번노드의 최단거리 배열의 값을 비교한다.
- 시작점에서 4번노드까지의 거리(12) + 4번 노드에서 5번노드까지의 거리(2) = 14
- 최단거리 배열의 값 = 23
비교한 결과, 5번노드의 값은 14로 업데이트 한다.

7) 탐색 종료
이렇게 모든 간선 정보를 확인하며 최단거리 배열을 업데이트 했다.
이제 1번노드에서 다른 노드로 가는 최단 경로 값들이 모두 최단거리 배열에 저장되어 있다.
이 알고리즘을 한번 수행하면 시작점 -> 목표지점에 대한 정보만 저장되어 있는 것이 아니라,
시작점에서 다른 모든 노드로의 최단경로 정보가 저장되게 된다.
기본적인 예제 문제
백준 1753번 : 최단 경로
2023.06.26 - [전체 글 보기] - [백준/Java] 1753번 : 최단경로 / 다익스트라(dijkstra)
(이미지 출처) Do it! 알고리즘 코딩 테스트 자바 편
http://www.yes24.com/Product/Goods/108571508
'자료구조_알고리즘 > Algorithm' 카테고리의 다른 글
| [Algorithm/Java] 플로이드 - 워셜(floyd - warshall) 알고리즘 (최단거리) (0) | 2023.06.28 |
|---|---|
| [Algorithm/Java] 벨만-포드 알고리즘 (최단거리, 음수 가중치 그래프) (1) | 2023.06.27 |
| [Algorithm/Java] greedy 그리디 알고리즘 (탐욕법) (0) | 2023.06.26 |
| [Algorithm/Java] 이진탐색 Binary Search / UpperBound / LowerBound (0) | 2023.06.04 |
| [JAVA / 수학 / 점화식] sqrt 제곱근 직접 구하는 알고리즘 (바빌로니아 법) (0) | 2023.06.02 |
