벨만-포드(bellman-ford-moore) 알고리즘
벨만 - 포드 알고리즘은 그래프에서 음수 가중치를 가진 간선이 있을 때 최단거리를 구하는 알고리즘이다.
- 다익스트라 알고리즘과 같이 특정 노드에서 다른 모든 노드까지의 최단 거리를 탐색한다.
- 다익스트라 알고리즘과 다르게 음수 간선이 포함되어 있어도 최단 경로를 구할 수 있다.
- 음수 사이클이 있을 경우 정상 동작하지 않는다.
- 음수 사이클의 존재 여부를 파악할 수 있다.
- 매번 모든 간선을 확인하기 때문에 다익스트라에 비해 느리다.
- 시간복잡도 : O(VE) => Vertex * Edge
벨만 - 포드 알고리즘 동작 원리
1. Edge 리스트로 그래프를 구현하고 최단경로 배열 초기화 하기
위에서 말했듯이 벨만 - 포드 알고리즘은 매번 모든 간선을 확인한다.
따라서 Edge 클래스를 만들어서 Edge 리스트로 그래프를 구현한다.
Edge 클래스는 일반적으로 출발노드, 종료노드, 가중치 이렇게 3개의 변수로 구성 되어있다.
다익스트라와 똑같이 최단경로 배열을 만들고, 출발 노드를 0 , 나머지 노드를 무한대로 초기화한다.

2. 모든 에지를 확인해 최단경로 배열 업데이트 하기
최단거리 리스트에서 업데이트 반복 횟수는 노드 개수 - 1이다.
A노드에서 B C노드를 거쳐 D 노드까지 도달하는 경우 Edge의 개수는 A - B, B - C, C - D로 3개이다.
따라서 N개의 노드에서 에지의 최대 개수는 N -1개이다.
업데이트 조건(방법)
출발 노드가 무한대 일 경우에는 건너뛰고,
도착노드의 최단경로 값 > 출발노드의 최단경로 값 + 두 노드를 잇는 간선의 가중치 일 경우 업데이트 한다.
if(distance[출발 노드] == 무한대){
continue;
}
if(distance[도착 노드] > distance[출발 노드] + 간선 가중치 ){
distance[도착 노드] = distance[출발 노드] + 간선 가중치;
}
3. 음수 사이클 확인
음수 사이클 유무를 확인하는 방법은 생각보다 매우 간단하다.
N-1번의 반복을 끝낸 뒤, 한 번 더 반복을 하며 모든 노드를 탐색한다.
마지막에 한번 더 반복할 때, 업데이트되는 노드가 있다면 해당 그래프에는 음수 사이클이 존재하는 것이다.
만약 음수 사이클이 존재하면, 이 사이클을 돌면 돌수록 최단경로 배열의 값이 감소되기 때문에 최단경로를 구할 수 없다.

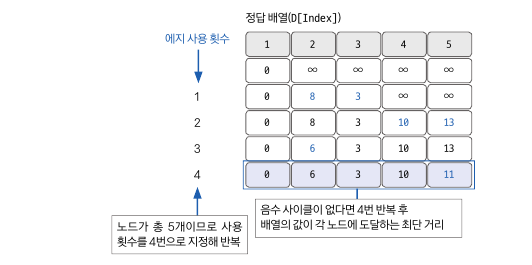
위의 그림에서 5개의 노드가 있기 때문에, N-1번인 4번 반복하면 최단경로 배열을 얻을 수 있다.
이후에 5번째 반복을 하여 변경된 값이 있는지 확인하면 음수사이클 여부를 알 수 있다.
그래서 실제 코드에서는 아래와 같이 반복을 N번 하며, N번째 반복에서 변경이 일어났는지 확인한다.
i == V 일 때는 N-1번의 반복을 끝내고 N번째 반복임을 나타낸다.
N번째 반복에서 업데이트 조건을 만족해서 if문 안으로 들어가게 되면, 변경이 일어났다는 뜻이므로 음수사이클이다.
boolean is MinusCycle = false;
for(int i = 0; i <= V ; i++){ //V : 노드의 개수
for(int j = 0; j < E; j++){// E : 간선의 개수
if(distance[출발 노드] == 무한대){
continue;
}
// 아래는 업데이트 조건을 만족할 때 실행됨
if(distance[도착 노드] > distance[출발 노드] + 간선 가중치 ){
distance[도착 노드] > distance[출발 노드] + 간선 가중치;
if(i == v){ //V번째의 반복에서 해당 업데이트 조건을 만족할 경우
isMinusCycle = true;
}
}
}
}[ 음수 사이클의 의미 ]
음수 사이클은 해당 사이클을 돌았을 때 가중치 값이 줄어드는 것이다.

위와 같은 음수 사이클이 있을 때, 4번 노드에서 출발해서 4 - 2 - 5를 한 바퀴 돌 때마다
시작노드에서 4번 노드로 가는 최단 경로는 1씩 감소하게 된다.
N-1번의 반복까지 최단경로 배열 1~5가 [ 0, 6, 3, 10, 11 ]이었다.
즉, 1번부터 4번까지의 최단 경로는 10이라는 뜻이다.
N번 반복하였을 때 4번 노드까지의 최단 경로는 9가 된다.
한번 더 반복하면 8이 되고, 한번 더 반복하면 7이 될 것이다.
따라서 음수 사이클이 존재한다는 것은 지금까지 행한 일련의 과정들이 무의미하게 된다는 것이다.
즉, 해당 그래프는 지금까지 얻어낸 최단경로 배열이 무의미하고, 최단 경로를 찾을 수 없는 그래프라는 뜻이 된다.
벨만-포드 알고리즘도 다익스트라 알고리즘과 마찬가지로 시작노드에서 다른 모든 노드까지의 최단경로 배열을 도출하게 된다.
따라서 벨만-포드 알고리즘을 한번 수행하고 나면, 원하는 모든 노드까지의 최단경로를 얻을 수 있게 된다.
최단거리를 구하는 알고리즘은 다익스트라, 벨만-포드, 플로이드-워셜 알고리즘이 있다.
이중에 음수 간선을 다루는 알고리즘은 벨만-포드 알고리즘 하나이다.
따라서 음수 간선이 등장할 경우에는 벨만-포드 알고리즘을 이용하면 된다.
(이미지 출처) Do it! 알고리즘 코딩 테스트 자바 편
http://www.yes24.com/Product/Goods/108571508
'자료구조 & 알고리즘' 카테고리의 다른 글
| [JAVA] 퀵 정렬 (Quick Sort) (0) | 2023.06.30 |
|---|---|
| [Algorithm/Java] 플로이드 - 워셜(floyd - warshall) 알고리즘 (최단거리) (0) | 2023.06.28 |
| [Algorithm/Java] 다익스트라(dijkstra) 알고리즘 (최단거리, 가중치 그래프) (1) | 2023.06.26 |
| [Algorithm/Java] greedy 그리디 알고리즘 (탐욕법) (0) | 2023.06.26 |
| [JAVA/자료구조] TreeSet : 정렬을 지원하는 Set (0) | 2023.06.18 |
