퀵 정렬 (Quick sort)
퀵 정렬은 기준값(pivot)을 선정해 해당 값보다 작은 데이터와 큰 데이터로 분류하는 것을 반복해 정렬하는 알고리즘이다. 시간복잡도가 비교적 빠르기 때문에 코딩테스트에서도 종종 응용한다.
평균 시간복잡도는 O(nlogn)이고, 최악은 O(n^2)이다.
이미 정렬돼 있는 배열에 적용할 때 최악의 시간복잡도를 가진다.
퀵 정렬(Quicksort)은 찰스 앤터니 리처드 호어가 개발한 정렬 알고리즘이다.
다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬에 속한다.
퀵 정렬의 내부 루프는 대부분의 컴퓨터 아키텍처에서 효율적으로 작동하도록 설계되어 있고, 대부분의 실질적인 데이터를 정렬할 때 제곱 시간이 걸릴 확률이 거의 없도록 알고리즘을 설계하는 것이 가능하다. 또한 매 단계에서 적어도 1개의 원소가 자기 자리를 찾게 되므로 이후 정렬할 개수가 줄어든다. 때문에 일반적인 경우 퀵 정렬은 다른 O(n log n) 알고리즘에 비해 훨씬 빠르게 동작한다. 그리고 퀵 정렬은 정렬을 위해 평균적으로 O(log n)만큼의 memory를 필요로 한다. 이는 재귀적 호출로 발생하는 것이며, 최악의 경우 O(n)의 공간복잡도를 보인다.
(위키백과)
이 글에서는 각 배열의 중간값을 기준값(pivot)으로 정하는 방식을 사용하겠다.
다른 방법으로는 왼쪽 끝 또는 오른쪽 끝을 pivot으로 삼는 방법이 있다.
핵심 이론
pivot을 중심으로 데이터를 계속 2개의 집합으로 나누면서 정렬하는 것이 퀵 정렬의 핵심이다.
처음에 보고 이해하기 어려울 수 있느니 바로 아래에 퀵정렬 예제와 같이 보는 것을 추천합니다.
퀵 정렬 과정
1. 데이터를 분할하는 기준값 pivot을 설정한다.
2. pivot을 기준으로 삼아 start와 end 포인트를 움직인다.
2-1. start < pivot 일때, start는 오른쪽으로 한 칸 이동한다.
2-2. end > pivot 일때, end는 왼쪽으로 한 칸 이동한다.
2-3. 움직일 수 없을 때 까지 2-1, 2-2를 반복한다.
즉, start는 pivot보다 크거나 같은 값을 찾을 때까지 움직이고, end는 pivot보다 작거나 같은 값을 찾을 때까지 움직인다.
3. start와 end 포인트의 값을 swap 하고, start포인트를 오른쪽으로 한 칸, end포인트를 왼쪽으로 한 칸 움직인다.
4. 위의 1~3의 과정을 (start<=end)를 만족하지 않을 때까지 반복한다.
5. 반복이 끝나면 pivot 값은 전체 리스트에서 자신의 자리를 찾은 것이 되고, 이제 전체 리스트를 pivot을 기준으로 두 개로 분리한다.
6. 반복이 끝났을 때의 start포인트가 가리키고 있는 위치가 두 번째 파티션의 첫 번째 인덱스가 되며, 각각 두 개로 나뉜 파티션에 대하여 (1~5번)의 과정을 반복한다.
퀵 정렬 예제
예제 배열

예제 1 : 첫 번째 반복
위와 같은 정렬되지 않은 배열이 있다.
- 중간값을 pivot으로 선정한다. (5)
- start와 end인덱스를 지정한다.
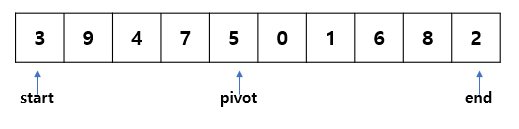
start < pivot의 경우 start를 한 칸씩 오른쪽으로 이동한다. ( pivot보다 큰 값을 찾을 때까지 이동 )
end > pivot의 경우 end를 한 칸씩 왼쪽으로 이동한다. (pivot보다 작은 값을 찾을 때까지 이동 )

start와 end 포인트를 더이상 움직일 수 없는 경우(원하는 값을 찾은 경우) 두 데이터를 swap 한다.( 2와 9 swap )
swap을 하고 나서 start, end 포인트를 한 칸씩 옮겨준다.


다시 위의 과정을 반복해, start, end 포인트가 멈출 때까지 이동시킨다. ( start=7, end=1)
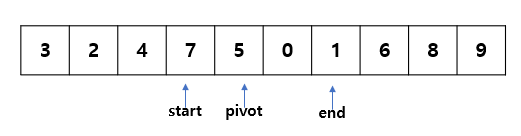
찾은 두 값을 swap 하고, 포인트를 한 칸씩 옮겨준다.


여기서 5의 위치는 start 포인트이면서 동시에 pivot 값이다.
start(5)는 5보다 작지 않기 때문에 움직이지 않는다.
0은 5보다 작으므로 움직이지 않는다. ( 0과 5 swap )
0과 5를 swap 하고, 포인트를 각각 움직여준다.
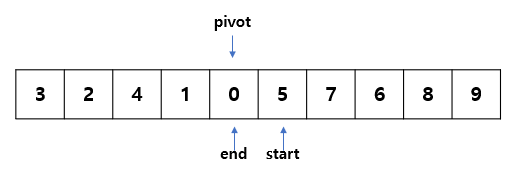
start와 end가 반복문의 조건에 맞지 않게 된다. (start <= end)
따라서 이 루프는 종료하고, start가 가리키고 있는 5를 기준으로 전체 배열을 나눈다. (파티션)
그렇게 되면 5는 오른쪽 파티션의 첫 번째 인덱스가 되고, 배열은 아래와 같이 나뉘게 된다.

이렇게 하나의 루프가 종료되면 pivot 값이었던 5는 전체 배열에서의 알맞은 위치를 찾게 된다.
이후, 두 개로 나뉜 파티션에서 위의 과정을 반복한다.
각각 중간값(pivot), start, end 포인트를 정하는 등..

두 번째 파티션에 대하여 한 번의 루프를 더 돌아보겠다.
예제 2 : 두 번째 반복

이제 start=5, pivot=6, end=9로 지정하여 새로 시작한다.
start는 pivot보다 큰 값이 나올 때까지, end는 pivot보다 작은 값이 나올 때까지 이동한다.
( end > pivot일 때 움직이므로 end포인트는 6에서 멈춘다)
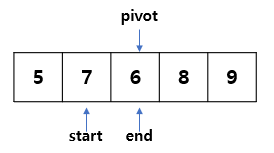
두 값을 swap 하고, 한 칸씩 움직인다.
움직이면 start <=end 조건을 만족하지 못하기 때문에 해당 루프는 끝난다.
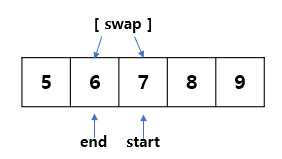
이 예제에서는 방금 전 두 번째 루프에서 정렬이 끝났지만, 정렬이 끝나지 않았을 경우 swap 후 start포인트 값인 7을 기준으로 다시 왼쪽, 오른쪽 파티션으로 나눠서 루프를 반복한다.
이렇게 재귀적으로 루프를 반복하다 보면 모든 값이 정렬된다.
Code
public class TEST {
public static void main(String[] args){
//입력 부 생략, 배열의 크기 n과 함께 배열에 넣을 값 입력
int[] arr = {3, 9, 4, 7, 5, 0, 1, 6, 8, 2};
int n = arr.length;
quickSort(arr,0,n-1);
System.out.println(Arrays.toString(arr));
}
public static void quickSort(int[] arr, int start, int end) {
int part2 = partition(arr, start, end); //part2 : 오른쪽 파티션의 시작점
//만약 start가 part2-1과 같으면 정렬할 필요가 없기때문에 if문에서 설정
if(start < part2 - 1){
quickSort(arr, start, part2-1);//end는 오른쪽 파티션의 시작점에서 왼쪽으로 한칸
}
//만약 part2의 시작점이 end와 같으면 정렬할 필요가 없기 때문에 if문에서 설정
if(part2 < end){
quickSort(arr, part2, end);
}
}
public static int partition(int[] arr, int start, int end){
int m = (start + end)/2;
int pivot = arr[m]; // 해당 파티션의 중간에 있는 값
//start와 end가 엇갈릴때까지 반복
while(start <= end){
// start가 피봇보다 작으면 start++ (피봇보다 큰 값이 나올때까지 반복)
while(arr[start] < pivot)start++;
//end가 피봇보다 크면 end-- (피봇보다 작은 값이 나올때까지 반복)
while(arr[end] > pivot)end--;
//start와 end가 서로 엇갈리지 않았으면 swap
if(start <= end){
swap(arr,start,end);
start++;
end--;
}
}
return start; //새로 나뉠 파티션의 첫번째 인덱스를 반환 (part2)
}
public static void swap(int[] arr, int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}(참고)
https://youtu.be/7BDzle2n47c
'자료구조 & 알고리즘' 카테고리의 다른 글
| [Algorithm/Java] 카운팅 정렬 (Counting sort) (0) | 2023.07.09 |
|---|---|
| [Algorithm/Java] DP(다이나믹 프로그래밍, 동적 계획법) (0) | 2023.07.01 |
| [Algorithm/Java] 플로이드 - 워셜(floyd - warshall) 알고리즘 (최단거리) (0) | 2023.06.28 |
| [Algorithm/Java] 벨만-포드 알고리즘 (최단거리, 음수 가중치 그래프) (1) | 2023.06.27 |
| [Algorithm/Java] 다익스트라(dijkstra) 알고리즘 (최단거리, 가중치 그래프) (1) | 2023.06.26 |
퀵 정렬 (Quick sort)
퀵 정렬은 기준값(pivot)을 선정해 해당 값보다 작은 데이터와 큰 데이터로 분류하는 것을 반복해 정렬하는 알고리즘이다. 시간복잡도가 비교적 빠르기 때문에 코딩테스트에서도 종종 응용한다.
평균 시간복잡도는 O(nlogn)이고, 최악은 O(n^2)이다.
이미 정렬돼 있는 배열에 적용할 때 최악의 시간복잡도를 가진다.
퀵 정렬(Quicksort)은 찰스 앤터니 리처드 호어가 개발한 정렬 알고리즘이다.
다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬에 속한다.
퀵 정렬의 내부 루프는 대부분의 컴퓨터 아키텍처에서 효율적으로 작동하도록 설계되어 있고, 대부분의 실질적인 데이터를 정렬할 때 제곱 시간이 걸릴 확률이 거의 없도록 알고리즘을 설계하는 것이 가능하다. 또한 매 단계에서 적어도 1개의 원소가 자기 자리를 찾게 되므로 이후 정렬할 개수가 줄어든다. 때문에 일반적인 경우 퀵 정렬은 다른 O(n log n) 알고리즘에 비해 훨씬 빠르게 동작한다. 그리고 퀵 정렬은 정렬을 위해 평균적으로 O(log n)만큼의 memory를 필요로 한다. 이는 재귀적 호출로 발생하는 것이며, 최악의 경우 O(n)의 공간복잡도를 보인다.
(위키백과)
이 글에서는 각 배열의 중간값을 기준값(pivot)으로 정하는 방식을 사용하겠다.
다른 방법으로는 왼쪽 끝 또는 오른쪽 끝을 pivot으로 삼는 방법이 있다.
핵심 이론
pivot을 중심으로 데이터를 계속 2개의 집합으로 나누면서 정렬하는 것이 퀵 정렬의 핵심이다.
처음에 보고 이해하기 어려울 수 있느니 바로 아래에 퀵정렬 예제와 같이 보는 것을 추천합니다.
퀵 정렬 과정
1. 데이터를 분할하는 기준값 pivot을 설정한다.
2. pivot을 기준으로 삼아 start와 end 포인트를 움직인다.
2-1. start < pivot 일때, start는 오른쪽으로 한 칸 이동한다.
2-2. end > pivot 일때, end는 왼쪽으로 한 칸 이동한다.
2-3. 움직일 수 없을 때 까지 2-1, 2-2를 반복한다.
즉, start는 pivot보다 크거나 같은 값을 찾을 때까지 움직이고, end는 pivot보다 작거나 같은 값을 찾을 때까지 움직인다.
3. start와 end 포인트의 값을 swap 하고, start포인트를 오른쪽으로 한 칸, end포인트를 왼쪽으로 한 칸 움직인다.
4. 위의 1~3의 과정을 (start<=end)를 만족하지 않을 때까지 반복한다.
5. 반복이 끝나면 pivot 값은 전체 리스트에서 자신의 자리를 찾은 것이 되고, 이제 전체 리스트를 pivot을 기준으로 두 개로 분리한다.
6. 반복이 끝났을 때의 start포인트가 가리키고 있는 위치가 두 번째 파티션의 첫 번째 인덱스가 되며, 각각 두 개로 나뉜 파티션에 대하여 (1~5번)의 과정을 반복한다.
퀵 정렬 예제
예제 배열

예제 1 : 첫 번째 반복
위와 같은 정렬되지 않은 배열이 있다.
- 중간값을 pivot으로 선정한다. (5)
- start와 end인덱스를 지정한다.

start < pivot의 경우 start를 한 칸씩 오른쪽으로 이동한다. ( pivot보다 큰 값을 찾을 때까지 이동 )
end > pivot의 경우 end를 한 칸씩 왼쪽으로 이동한다. (pivot보다 작은 값을 찾을 때까지 이동 )

start와 end 포인트를 더이상 움직일 수 없는 경우(원하는 값을 찾은 경우) 두 데이터를 swap 한다.( 2와 9 swap )
swap을 하고 나서 start, end 포인트를 한 칸씩 옮겨준다.


다시 위의 과정을 반복해, start, end 포인트가 멈출 때까지 이동시킨다. ( start=7, end=1)

찾은 두 값을 swap 하고, 포인트를 한 칸씩 옮겨준다.


여기서 5의 위치는 start 포인트이면서 동시에 pivot 값이다.
start(5)는 5보다 작지 않기 때문에 움직이지 않는다.
0은 5보다 작으므로 움직이지 않는다. ( 0과 5 swap )
0과 5를 swap 하고, 포인트를 각각 움직여준다.

start와 end가 반복문의 조건에 맞지 않게 된다. (start <= end)
따라서 이 루프는 종료하고, start가 가리키고 있는 5를 기준으로 전체 배열을 나눈다. (파티션)
그렇게 되면 5는 오른쪽 파티션의 첫 번째 인덱스가 되고, 배열은 아래와 같이 나뉘게 된다.

이렇게 하나의 루프가 종료되면 pivot 값이었던 5는 전체 배열에서의 알맞은 위치를 찾게 된다.
이후, 두 개로 나뉜 파티션에서 위의 과정을 반복한다.
각각 중간값(pivot), start, end 포인트를 정하는 등..

두 번째 파티션에 대하여 한 번의 루프를 더 돌아보겠다.
예제 2 : 두 번째 반복

이제 start=5, pivot=6, end=9로 지정하여 새로 시작한다.
start는 pivot보다 큰 값이 나올 때까지, end는 pivot보다 작은 값이 나올 때까지 이동한다.
( end > pivot일 때 움직이므로 end포인트는 6에서 멈춘다)

두 값을 swap 하고, 한 칸씩 움직인다.
움직이면 start <=end 조건을 만족하지 못하기 때문에 해당 루프는 끝난다.

이 예제에서는 방금 전 두 번째 루프에서 정렬이 끝났지만, 정렬이 끝나지 않았을 경우 swap 후 start포인트 값인 7을 기준으로 다시 왼쪽, 오른쪽 파티션으로 나눠서 루프를 반복한다.
이렇게 재귀적으로 루프를 반복하다 보면 모든 값이 정렬된다.
Code
public class TEST {
public static void main(String[] args){
//입력 부 생략, 배열의 크기 n과 함께 배열에 넣을 값 입력
int[] arr = {3, 9, 4, 7, 5, 0, 1, 6, 8, 2};
int n = arr.length;
quickSort(arr,0,n-1);
System.out.println(Arrays.toString(arr));
}
public static void quickSort(int[] arr, int start, int end) {
int part2 = partition(arr, start, end); //part2 : 오른쪽 파티션의 시작점
//만약 start가 part2-1과 같으면 정렬할 필요가 없기때문에 if문에서 설정
if(start < part2 - 1){
quickSort(arr, start, part2-1);//end는 오른쪽 파티션의 시작점에서 왼쪽으로 한칸
}
//만약 part2의 시작점이 end와 같으면 정렬할 필요가 없기 때문에 if문에서 설정
if(part2 < end){
quickSort(arr, part2, end);
}
}
public static int partition(int[] arr, int start, int end){
int m = (start + end)/2;
int pivot = arr[m]; // 해당 파티션의 중간에 있는 값
//start와 end가 엇갈릴때까지 반복
while(start <= end){
// start가 피봇보다 작으면 start++ (피봇보다 큰 값이 나올때까지 반복)
while(arr[start] < pivot)start++;
//end가 피봇보다 크면 end-- (피봇보다 작은 값이 나올때까지 반복)
while(arr[end] > pivot)end--;
//start와 end가 서로 엇갈리지 않았으면 swap
if(start <= end){
swap(arr,start,end);
start++;
end--;
}
}
return start; //새로 나뉠 파티션의 첫번째 인덱스를 반환 (part2)
}
public static void swap(int[] arr, int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}(참고)
https://youtu.be/7BDzle2n47c
'자료구조 & 알고리즘' 카테고리의 다른 글
| [Algorithm/Java] 카운팅 정렬 (Counting sort) (0) | 2023.07.09 |
|---|---|
| [Algorithm/Java] DP(다이나믹 프로그래밍, 동적 계획법) (0) | 2023.07.01 |
| [Algorithm/Java] 플로이드 - 워셜(floyd - warshall) 알고리즘 (최단거리) (0) | 2023.06.28 |
| [Algorithm/Java] 벨만-포드 알고리즘 (최단거리, 음수 가중치 그래프) (1) | 2023.06.27 |
| [Algorithm/Java] 다익스트라(dijkstra) 알고리즘 (최단거리, 가중치 그래프) (1) | 2023.06.26 |
