[JAVA/자료구조] 그래프(Graph)의 개념, 탐색, 구현

그래프(Graph)

그래프는 정점 와 간선로 이루어진 자료구조이다.

이는 트리(Tree)와 같지만, 트리는 Acyclic(사이클 x)인 반면 그래프는 사이클이 존재한다. (Cyclic)

각 정점(Vertex)들이 간선(Edge)들로 연결되어, 연결된 정점 간의 관계를 표현할 수 있는 자료구조이다.

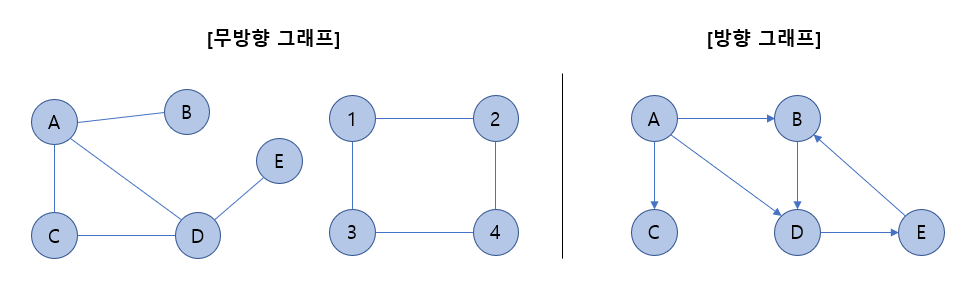
그래프의 구조(용어)

• 정점(Vertex) : 노드 
• 간선(Edge) : 각 노드간의 연결 선 ( = link, branch)
• 인접 정점(Adjacent Vertex) : 간선 하나만을 통해 바로 연결되어 있는 정점 (정점 1과 정점 4는 인접정점 x)

무방향 그래프

• 정점의 차수(Degree) : 하나의 정점에 인접한 정점의 수 (정점 1의 차수는 2 ), (정점 A의 차수는 3)
  • 무방향 그래프에서 모든 정점 차수의 합은 그래프 전체 간선 수의 2배이다.

방향 그래프

• 진입 차수(In-Degree) : 방향 그래프에서 각 정점으로 외부에서 들어오는 간선의 수 (정점 B의 진입 차수는 2)
• 진출 차수(Out-Degree) : 방향 그래프에서 각 정점에서 외부로 나가는 간선의 수 (정점 A의 진출 차수는 3)

경로

• 경로 길이(Path length) : 경로를 구성하는데 사용된 간선의 수
  • 방향그래프에서 A에서 E로 가는 경우는 여러가지이고, 각각의 경로길이는 다르다.
  • A -> B -> D -> E : 경로길이=3
  • A -> D -> E : 경로길이=2
• 단순 경로(Simple path) : 경로 중에서 반복되는 정점이 없는 경우
• 사이클(Cycle) : 단순경로로 한 바퀴 돌아서 다시 같은 노드로 돌아오는 경우
  • 만약 방향그래프 이미지에서 A - D간의 간선이 D에서 A를 향하고 있다면, A -> B -> D -> A를 사이클이라고 한다.

---

그래프와 트리 비교

	그래프	트리
정의	노드와 간선을 하나로 모아놓은 자료구조	그래프의 한 종류 (방향성이 있는 비순환 그래프)
방향성	방향 그래프 , 무방향 그래프	방향 그래프
사이클	Cyclic  순환그래프(Cyclic), 비순환 그래프 모두 가능(Acyclic)	Acyclic 비순환 그래프(Acyclic Graph)
루트 노드	루트 노드의 개념이 없음	가장 위에 하나의 루트 노드가 존재
부모-자식	부모-자식의 개념이 없음	부모-자식 관계로 이루어짐 모든 자식 노드는 한개의 부모 노드만을 가짐
모델	네트워크 모델	계층 모델
순회	DFS, BFS	Pre-order, In-order, Post-order / Level-order
간선의 수	그래프마다 다름	노드가 N개인 트리는 항상 N-1개의 간선을 가짐
경로	2개 이상의 경로 가능	두 노드간의 경로는 1개만 가질 수 있음

---

그래프의 종류

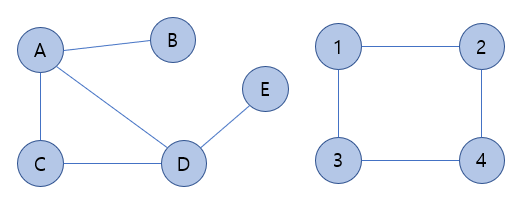
1. 무방향 그래프(Undirected Graph)

• 두 정점을 연결하는 간선에 방향이 없는 그래프
• 정점 A - B 간선의 표현 : (A, B) = (B, A)

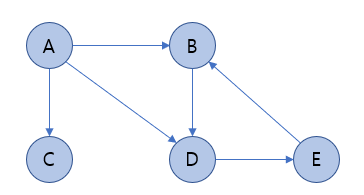
2. 방향 그래프(Directed Graph)

• 두 정점을 연결하는 간선에 방향이 있는 그래프
• 지정된 방향으로만 이동 가능
• 정점 A - B 간선의 표현 : <A, B> ≠ <B, A>

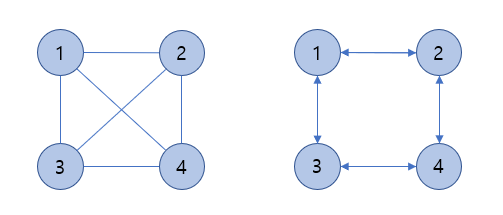
3. 완전 그래프(Complete Graph)

• 모든 정점이 서로 연결되어 최대 간선 수를 갖는 그래프
• 정점이 N개일 경우, 간선 수는 N(N-1) / 2 개

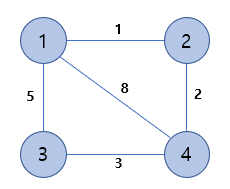
4. 가중치 그래프(Weight Graph)

• 정점을 연결하는 간선에 가중치(weight)를 할당한 그래프

---

그래프 탐색

1. DFS : 깊이 우선 탐색 (Depth First Search)

• 그래프의 모든 노드를 방문하는 완전 탐색 방식이다.
• 임의의 시작노드에서 출발하여 한쪽 분기를 정해서 최대 깊이까지 탐색을 마친 후, 다른쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘이다.
• 재귀함수 또는 Stack 자료구조를 이용한다.

2023.05.08 - [Algorithm/탐색 (search)] - DFS(깊이 우선 탐색)

DFS(깊이 우선 탐색)

---

2. BFS : 너비 우선 탐색(Breadth First Search)

• 그래프의 모든 노드를 방문하는 완전 탐색 방식이다.
• 임의의 시작노드에서 시작 노드를 기준으로 가장 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘이다.
• FIFO 탐색 -> Queue 자료구조를 이용한다.
• 목표 노드에 도착하는 경로가 여러 개일 때 최단 경로를 보장한다.

2023.05.08 - [Algorithm/탐색 (search)] - BFS(깊이 우선 탐색)

BFS(너비 우선 탐색)

---

그래프의 구현

인접 행렬 (Adjacency Matrix)

• 2차원 배열을 이용한다.
• 노드수가 N개 일때, N x N의 int 행렬 또는 boolean 행렬을 만들어서, 연결 상태 값을 설정한다.
• matrix[ i ][ j ] == true 라면 i -> j로의 간선이 있다는 뜻이다. (int 행렬의 경우 1 = true, 0 = false)

인접 행렬 방식의 특징

• 배열로 구성되어 있기 때문에, 간선 정보 조회가 빠름 O(1)
• 간선의 개수와 무관하게 항상 N^2개의 메모리 공간을 차지한다.
• 인접 행렬에서는 인접한 노드를 찾기 위해서는 모든 노드를 전부 순회해야 한다.

---

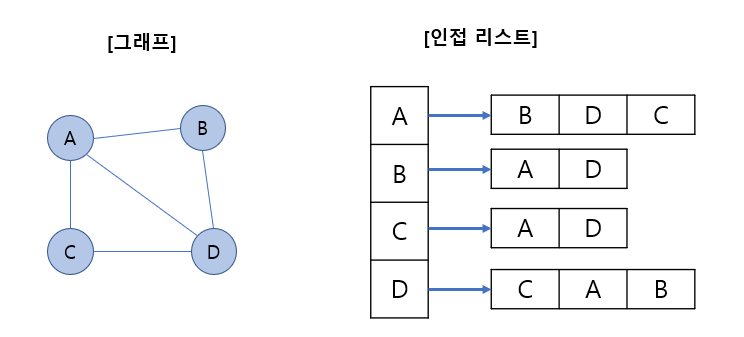
인접 리스트 (Adjacency List)

인접 리스트로 그래프를 표현하는 것이 일반적인 방법이다.

• 연결리스트를 이용하여 모든 정점을 인접리스트에 저장한다.
• ArrayList 형 배열( ArrayList<Integer>[] )을 만들어서 연결된 노드를 각각 저장한다.

인접 리스트 방식의 특징

• 연결된 노드의 개수와 딱 맞는 크기로 리스트를 만들기 때문에 메모리 사용량이 상대적으로 적다.
• 노드의 추가 삭제가 빠르다.
• 간선 정보 확인이 상대적으로 오래걸린다.

---

인접 행렬과 인접 리스트 중 선택 방법

인접 행렬

• 그래프 내에 적은 숫자의 간선만을 가지는 희소 그래프(Sparse Graph)의 경우

즉, 노드의 개수가 적고 간선의 수가 많을 때 더 낫다.

인접 리스트

• 그래프에 간선이 많이 존재하는 밀집 그래프(Dense Graph)의 경우

즉, 노드의 개수가 많고 간선의 수가 적을 때 더 낫다.

 

---

참고
https://gmlwjd9405.github.io/2018/08/13/data-structure-graph.html
https://leejinseop.tistory.com/43